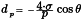Appendix XVII R. Porosity and Pore-size Distribution of Solids by Mercury Porosimetry
INTRODUCTION
In general, different types of pores may be pictured as apertures, channels or cavities within a solid body, or as space (i.e. interstices or voids) between solid particles in a bed, compact or aggregate. Porosity is a term that is often used to indicate the porous nature of solid material, and is more precisely defined as the ratio of the volume of accessible pores and voids to the total volume occupied by a given amount of the solid. In addition to the accessible pores, a solid may contain closed pores, which are isolated from the external surface and into which fluids are not able to penetrate. The characterisation of closed pores, i.e. cavities with no access to an external surface, is not covered in this chapter.
Porous materials may take the form of fine or coarse powders, compacts, extrudates, sheets or monoliths. Their characterisation usually involves the determination of the total pore volume or porosity as well as the pore-size distribution.
It is well established that the performance of a porous solid (e.g. its strength, reactivity, permeability or adsorbent power) is dependent upon its pore structure. Many different methods have been developed for the characterisation of pore structure. In view of the complexity of most porous solids, it is not surprising to find that the results obtained are not always in agreement and that no single technique can be relied upon to provide a complete picture of the pore structure. The choice of the most appropriate method depends on the application of the porous solid, its chemical and physical nature and the range of pore-size.
This chapter provides guidance for measurement of porosity and pore-size distribution by mercury porosimetry. It is a comparative test, usually destructive, in which the volume of mercury penetrating a pore or void is determined as a function of an applied hydrostatic pressure, which can be related to a pore diameter. Other information such as pore shape and inter-connectivity, the internal and external surface area, powder granulometry, bulk and tapped density could also be inferred from volume-pressure curves; however, these aspects of the technique do not fall under the scope of this chapter.
Practical considerations presently limit the maximum applied absolute pressure reached by some equipment to about 400 MPa, corresponding to a minimum equivalent pore diameter of approximately 0.003 µm. The maximum diameter will be limited for samples having a significant depth due to the difference in hydrostatic head of mercury from the top to the bottom of the sample. For most purposes this limit may be regarded as 400 µm.
Inter-particle and intra-particle porosity can be determined, but the method does not distinguish between these porosities where they co-exist.
The method is suitable for the study of most porous materials. Samples that amalgamate with mercury, such as certain metals, may be unsuitable for this technique or may require a preliminary passivation. Other materials may deform or compact under the applied pressure. In some cases it may be possible to apply sample-compressibility corrections and useful comparative data may still be obtained.
Mercury porosimetry is considered to be comparative, as for most porous media a theory is not available to allow an absolute calculation of results of pore-size distribution. Therefore this technique is mainly recommended for development studies.
Mercury is toxic. Appropriate precautions must be observed to safeguard the health of the operator and others working in the area. Waste material must also be disposed of in a suitable manner, according to local regulations.
principle
The technique is based on the measurement of the mercury volume intruded into a porous solid as a function of the applied pressure. The measurement includes only those pores into which mercury can penetrate at the pressure applied.
A non-wetting liquid penetrates into a porous system only under pressure. The pressure to be applied is in inverse proportion to the inner diameter of the pore aperture. In the case of cylindrical pores, the correlation between pore diameter and pressure is given by the Washburn equation:
| dp | = | pore diameter, in metres; |
| σ | = | surface tension, in newtons per metre; |
| θ | = | contact angle of mercury on the sample, in degrees; |
| p | = | applied pressure, in pascals. |
APPARATUS
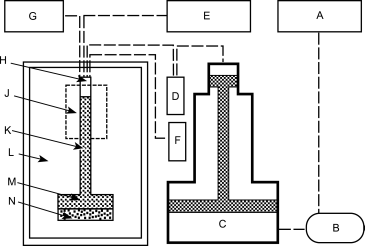
The sample holder, referred to as penetrometer or dilatometer, has a calibrated capillary tube, through which the sample can be evacuated and through which mercury can enter. The capillary tube is attached to a wider tube in which the test sample is placed. The change in the volume of mercury intruded is usually measured by the change in capacitance between the mercury column in the capillary tube and a metal sleeve around the outside of the capillary tube. If precise measurements are required the expected total void and pore volume of the sample should be between 20 per cent and 90 per cent of the internal volume of the capillary tube. Since different materials exhibit a wide range of open porosities, a number of penetrometers with different capillary tube diameters and sample volumes may be required. A typical set-up for a mercury porosimeter instrument is given in Figure 2.9.32.-1. The porosimeter may have separate ports for high- and low-pressure operation, or the low-pressure measurement may be carried out on a separate unit.
The pressure range is typically 4-300 kPa for low-pressure operation and above 300 kPa for high-pressure operation, depending on the design of the particular apparatus and on the intended use.
| A. Low-pressure hydraulic fluid reservoir | E. High-pressure hydraulic fluid reservoir | J. Penetration volume indicator | N. Sample | ||
| B. Hydraulic pump | F. Vacuum pump with gauge | K. Capillary tube | |||
| C. Pressure multiplier | G. Mercury reservoir | L. High pressure chamber | |||
| D. Pressure transducer | H. Oil | M. Mercury |
method
Sample preparation
The sample is pre-treated to remove adsorbed material that can obscure its accessible porosity, for example by heating and/or evacuation, or by flowing inert gas. It may be possible to passivate the surface of wettable or amalgam-forming solids, for example by producing a thin layer of oxide, or by coating with stearate.
The sample of the pre-treated solid is weighed and transferred to the penetrometer. The pore system of the sample is then degassed in a vacuum to a maximum residual pressure of 7 Pa.
Filling the penetrometer with mercury
The mercury used is of analytical quality. Overlay the sample with mercury under vacuum. The vacuum is required to ensure the transfer of mercury from the reservoir to the penetrometer. In a filled penetrometer the filling pressure comprises the applied pressure plus the pressure contribution created by the head of mercury contacting the sample. A typical filling pressure would be about 4 kPa. The hydrostatic pressure of the mercury over the sample may be minimised by filling the penetrometer in the horizontal position.
Low-pressure measurement
Admit air or nitrogen in a controlled manner to increase the pressure either in stages corresponding to the particular pore sizes of interest, or continuously at a slow rate. The concomitant change in the length of the mercury column in the capillary tube is recorded. When the maximum required pressure has been reached, return to atmospheric pressure.
High-pressure measurement
After measurement at low pressure, the penetrometer filled with mercury is transferred to the high-pressure port or unit of the instrument and overlaid with hydraulic fluid. Mercury is intruded into the pore system via the hydraulic fluid. Increase the pressure in the system to the maximum pressure reached in the low-pressure measurement and record the intrusion volume at this pressure, since subsequent intrusion volumes are calculated from this initial volume. Increase the pressure either in stages corresponding to the particular pore sizes of interest, or continuously at a slow rate. The fall in the mercury column is measured up to the maximum required pressure. If required the pressure may be decreased either in stages or continuously at a slow rate to determine the mercury extrusion curve.
Corrections are made to take account of changes in the volume of the mercury, the penetrometer and other components of the volume detector system under elevated pressure. The extent of the corrections may be determined by means of blank measurements under the same conditions.
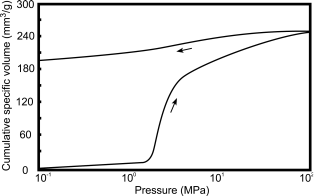
An experimentally determined volume-pressure curve is shown in Figure 2.9.32.-2.
reporting of results
The pressure readings can be converted to pore diameters by means of the Washburn equation or by another model.
The surface tension of mercury (σ) depends not only on the temperature, but also, in the case of markedly curved surfaces areas, on the radius of curvature. In general, values between 0.41 N⋅m-1 and 0.52 N⋅m-1 are measured at room temperature. If the value is not known, σ = 0.48 N⋅m-1 can be used.
The contact angle of mercury (θ) in most cases is more than 90°. It may be determined using a contact angle instrument. If the value is not known, θ = 130° can be used. The values of contact angle and surface tension and the model used in the calculation are reported.
Visualisation of the data can be done with several types of graphs. Frequently, in a graphical representation the pore diameter is plotted on the abscissa and the intruded volume per sample mass on the ordinate to give the pore-size distribution. It is appropriate here to choose a logarithmic scale for the abscissa (see Figure 2.9.32.-3). The spaces between the particles of the solid sample are included as pores in the calculation. If the pores differ in size from the voids, the latter can be separated by choosing the appropriate pore-size range.
Extrusion curves may not be used for calculating the pore-size distribution (for hysteresis, see Figure 2.9.32.-2), because an intruded part of the mercury always remains in the pore system. The retention ratio may however be useful for the qualitative characterisation of pores that are only accessible via narrow openings (‘ink-bottle pores′).
Most common characteristic values, such as the total intruded specific volume and the mean and median pore diameters, are calculated from the pore-size distribution. Moreover, sufficient information must be documented about the sample, the sample preparation, the evacuation conditions and the instrument used.
control of instrument performance
As mercury porosimetry is considered to be used as a comparative test, no details are given in this chapter. However, it is recommended that a stable comparison material is tested on a regular basis to monitor instrument calibration and performance.